20240611_머신러닝_가중치를 찾기 위한 경사하강법
in 파이썬
가중치에 따라 예측 결과가 바뀐다. 예측 정확도를 높히기 위해 Loss를 최소화 하는 가중치를 찾는 방법중에 경사하강법에 대해 알아봤다.
손실함수 (Loss function)에 따라 오차 구하는 식
- 총 오차를 계산하는 수식을 손실함수라고 부르며, 상황에 따라 다양한 수식이 있음
- 예측값 - 결과값을 제곱해서 평균치를 구하는 방식도 있음(양수,음수따문에)
평균제곱오차
- 각 데이터에 예측값과 실제값의 차이를 구하고 그 차이를 제곱한 뒤, 모든 차이의 제곱값의 합의 평균을 구하는 오차 계산 공식
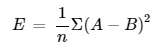
- E(=Loss): 평균 제곱 오차 (Mean Squared Error, MSE)
- 𝑛: 데이터 포인트의 개수
- ∑: 합을 나타내는 시그마 기호, 모든 데이터 포인트에 대해 합을 구함
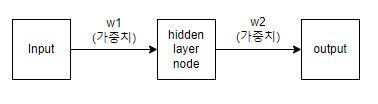
- A: 예측값 (예상값 = Input * w1)
- B: 실제값 (결과값 = output)
- (𝐴−𝐵)^2 : 예측값과 실제값의 차이를 제곱한 값
Loss(위 식에서 평균 제곱 오차=E)를 최소화 하는 가중치 값 찾기
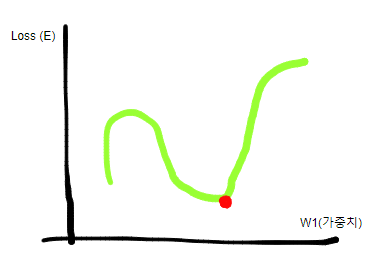
- 가중치를 뭘 넣냐에 따라서 E(Loss) 값이 바뀌는데, 이 때 가장 Loss를 최적화 하는 가중치를 찾아야함.
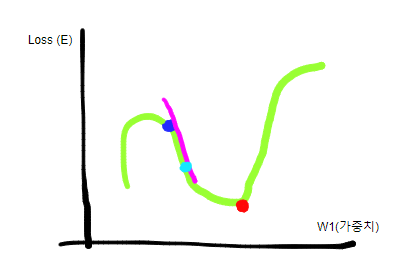
- 그래프로 그리면 대충 이렇게 나올 수 있는데, 이 때 빨간점에 해당하는 w1이 Loss를 최소화하는 가중치가 될것이다.
경사하강법(Gradient Descent) 알고리즘
- 위와같이 가중치가 하나라면 2차원 그래프로 표시할 수 있을텐데, 뉴럴네트워크의 경우 가중치가 무수히 많아 n차원이 될 것이다. 이 때 Loss를 최소화 하는 가중치를 찾는 방법이
경사하강법이다.
구하는 방법
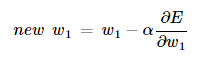
- new w1 : 새로운 가중치
- w1 : 현재 가중치
- α : Learning Rate - 가중치를 업데이트 할 때 한번에 이동할 양을 결정하는 상수
- 분수 : 가중치에따라 얼마나 변하는지 나타내는 값 (대충 기울기)
- 새로운w = w1 - (w1 값의 접선의 기울기 * learning rate)
- 이해를 돕기위한 그림
- 파란점(w1) - 보라선(w1값의 접선의기울기) = 하늘색점(새로운w)
learning rate
- 경사하강법에서 기울기가 0이 되는 순간 총손실이 더이상 줄어들지 않는다. 이 때가 최저점이 아님에도 기울기가 0이면 잘못된 결과를 도출(
local minima*특정 구간에서 함수값이 최소값이 되는 현상)하게 되므로 별도로 정한 상수값(learning rate)을 곱해줘서 이 문제를 방지한다. - 보통 작은숫자(0.001)등부터 넣어보면서 바꿔준다.
- learning rate optimizer를 사용해서(알고리즘인듯) learning rate를 정해주는 방법도 있다. (보통 Adam 모델을 쓴다는듯)
이거를 딥러닝한테 이렇게 시키면 된다.
- 랜덤 w값을 정함
- 정해진 w값으로 총손실 E를 계산한다.
- 경사하강법으로 새로운 w를 구한다
- 2~3번 과정을 총손실 E가 줄어들지 않을때까지 반복한다.